Definition Of A Perfect Square
In mathematics, we might have encounter different types of numbers such equally even, odd, prime, composite, etc. However, there is a particular type of number, i.e. a perfect square. These can be identified and expressed with the assistance of factorisation of a number. In this article, you will learn the definition of perfect square numbers, notation, the listing of these numbers between 1 and 100 and and so on.
Perfect Squares Definition
An integer that can be expressed equally the square of another integer is called a perfect square. In other words, it is defined as the production of some integer with itself.

Perfect Square Numbers
Nosotros know that the square of a number is that number times itself. In other words, the perfect squares are the squares of the whole numbers such as 1 or 1two, 4 or 22, ix or iii2, 16 or 42, 25 or v2 and and so on.
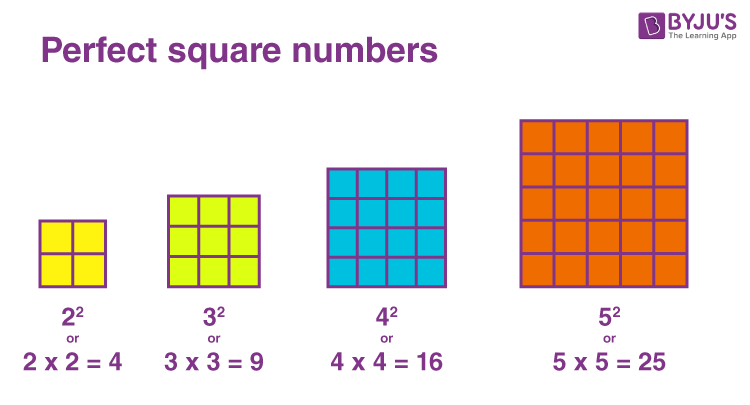
Also, get the perfect square calculator here.
Perfect Squares from ane to 100
Below shows the listing of perfect squares from i to 100 along with their factors (product of integers).
| Perfect foursquare numbers from 1 to 100 | ||||
| 1 | = | one × 1 | = | 12 |
| 4 | = | 2 × 2 | = | 2ii |
| 9 | = | 3 × 3 | = | 32 |
| xvi | = | 4 × four | = | 4ii |
| 25 | = | five × 5 | = | 52 |
| 36 | = | 6 × half-dozen | = | 62 |
| 49 | = | vii × 7 | = | 72 |
| 64 | = | viii × 8 | = | eightii |
| 81 | = | ix × 9 | = | 92 |
| 100 | = | x × 10 | = | x2 |
Perfect Squares Listing
The perfect squares table is given below in terms of squares of numbers from 1 to 50.
| 1 = 1two | 441 = 21ii | 1681 = 412 |
| 4 = 22 | 484 = 222 | 1764 = 422 |
| 9 = 32 | 529 = 232 | 1849 = 43two |
| 16 = 42 | 576 = 242 | 1936 = 442 |
| 25 = 52 | 625 = 252 | 2025 = 45two |
| 36 = 62 | 676 = 26ii | 2116 = 462 |
| 49 = 72 | 729 = 27two | 2209 = 47ii |
| 64 = 82 | 784 = 282 | 2304 = 482 |
| 81 = 9two | 841 = 292 | 2401 = 492 |
| 100 = 10ii | 900 = xxx2 | 2500 = 502 |
| 121 = eleven2 | 961 = 31ii | 2601 = 51two |
| 144 = 12ii | 1024 = 322 | 2704 = 522 |
| 169 = 132 | 1089 = 33ii | 2809 = 532 |
| 196 = 142 | 1156 = 342 | 2916 = 54ii |
| 225 = xvtwo | 1225 = 35two | 3025 = 552 |
| 256 = 162 | 1296 = 36two | 3136 = 56two |
| 289 = 172 | 1369 = 372 | 3249 = 57ii |
| 324 = 18ii | 1444 = 382 | 3364 = 58ii |
| 361 = 192 | 1521 = 392 | 3481 = 592 |
| 400 = 20ii | 1600 = xlii | 3600 = 60ii |
From this nosotros tin can derive the formula to get the difference between any perfect foursquare number and its predecessor. This is given by the equation,
n2 − (n − one)ii = 2n − 1
However, it is possible to count the number of square numbers using the formula,
ntwo = (n − 1)2 + (n − 1) + n
Perfect Squares Examples
Perfect square numbers are not only limited to the numerals simply likewise be in algebraic identities and polynomials. These can be identified with the assistance of a factorisation technique.
Algebraic identities equally perfect squares:
a2 + 2ab + b2 = (a + b)2
a2 – 2ab + bii = (a – b)2
Polynomials as perfect squares:
Let us take the polynomial x2 + 10x + 25.
At present, factorise the polynomial.
x2 + 10x + 25 = 102 + 5x + 5x + 25
= x(ten + 5) + 5(x + v)
= (x + 5)(x + 5)
= (ten + v)ii
Let us accept some other example:
x2 – 12x + 36 = x2 – 6x – 6x + 36
= 10(10 – 6) – 6(x – 6)
= (ten – half-dozen)(10 – vi)
= (ten – 6)two
From the above examples, we can say that x2 + 10x + 25 and 102 – 12x + 36 are chosen perfect square trinomials.
Perfect Squares Chart
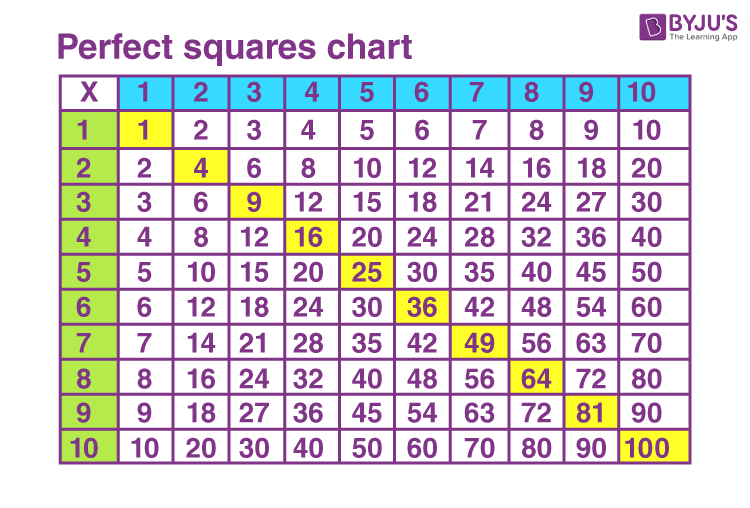
How many Perfect Squares betwixt i and 100
There are eight perfect squares betwixt 1 and 10 (i.due east., excluding 1 and 10).
They are four, 9, 16, 25, 36, 49, 64 and 81.
However, there are ten perfect squares from 1 to 10. They are 1, four, 9, sixteen, 25, 36, 49, 64, 81 and 100.
How many Perfect Squares between 1 and g
There are 30 perfect squares between ane and g. They are 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400, 441, 484, 529, 576, 625, 676, 729, 784, 841, 900 and 961.
Is 216 a perfect square
A number is a perfect square or a square number if its square root is an integer, which means it is an integer'south product with itself. Every bit we know, the square root of 216 is approximately equal to fourteen.697. Hither, the square root of 216 is not an integer. Hence, information technology is clear that 216 is not a perfect square number.
Definition Of A Perfect Square,
Source: https://byjus.com/maths/perfect-squares/
Posted by: jamesfourgaver.blogspot.com


0 Response to "Definition Of A Perfect Square"
Post a Comment