Cos Squared Plus Sine Squared

Different means of viewing cos²(t) + sin²(t) = 1

by Walter Vannini

Introduction
Triangles
Unit Circle
Root Mean Square
Rotation Matrix
Determinant
Orthonormal Footing
Combinatorial Identities
Exponential Function
Algebra
Factorization
Parametrized Curve Derivatives
Integral
Conservation Of Energy
Hyperbolic Analogues
Feedback

Introduction

Nosotros will explore various interpretations of the above identity. Later parts of this essay don't often depend on earlier parts, so please feel gratis to skim by incomprehensible text until you find something y'all're comfy with.

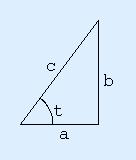
Triangles

The usual way the identity is understood is via Pythagoras' theorem. In a right angled triangle with sides a,b,c, and angle t at the vertex where a and c meet, cos(t) is by definition a/c, sin(t) is by definition b/c , and so cos²(t) + sin²(t) is (a/c)²+(b/c)^two , which by uncomplicated algebraic manipulation is (a^two+bⁱⁱ)/cⁱⁱ . Pythagoras' theorem states that a²+b² is c^two , and and then this simplifies to 1.

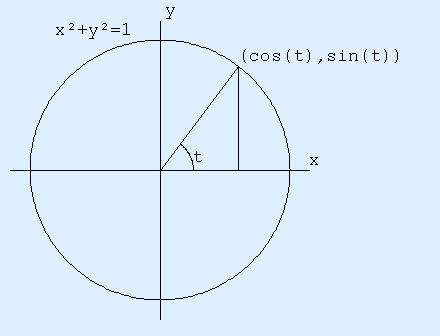
Unit Circle

Traditionally (ie. the fashion I learned information technology), the side by side footstep is to realize that the unit circumvolve centered at (0,0) in the (10,y) airplane is defined by ten²+yⁱⁱ=1. The in a higher place identity tin then exist interpreted as maxim that the point (cos(t), sin(t)) is on the unit circumvolve. Furthermore, this approach leads to a definition of cos(t) and sin(t) for all real t.

Root Mean Foursquare

Another manner to understand this identity is via the trigonometric identities

	cos²(x)	=	i/2	+	(1/2)	cos(2x)
	sin²(x)	=	one/2	-	(i/2)	cos(2x)

Incidentally, these identities pretty much leap out at you lot from looking at the graphs of y = cos^two(10) and y = sin²(10).

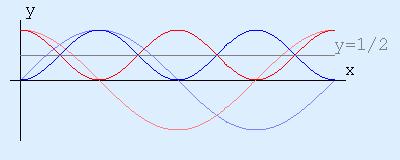
Another way to look at information technology is to retrieve that the root mean square of cos is 1/√2, as is the root mean square of sin. This means that cos² is 1/2 + variation, and sin² is 1/two + variation, and amazingly the variation of cos² is precisely the negative of the variation of sin² . Actually, this does fit in with the fact that sin and cos are but phase-shifted versions of each other, and so that sin² and cos² are phase-shifted versions of each other, and so their variations should be somehow related.
Anyway, nosotros now have that cos²(t)+sinⁱⁱ(t) is of the course (ane/two + deviation) + (one/2 - deviation), and so this is 1.

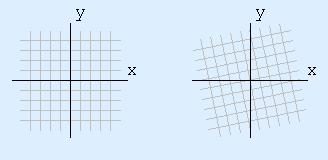
Rotation Matrix

Yet another manner to empathise the identity is via ii by 2 matrices. The linear matrix that represents an anticlockwise rotation past angle t is

`cos(t)`	`-sin(t)`
`sin(t)`	`cos(t)`

Determinant

The matrix

has determinant ad-bc, so the rotation matrix has determinant cos(t)cos(t)-(-sin(t))sin(t), which is cos(t)cos(t)+sin(t)sin(t) , ie cos^two(t)+sin^two(t). The determinant of a foursquare matrix has a uncomplicated geometric interpretation. Information technology is the area scaling factor. For a rotation, expanse is unchanged, and then the determinant has to be i. Then the identity cos²(t)+sin² (t)=ane can be interpreted as expressing the rather obvious fact that rotating an object in the (x,y) plane does not change its area.

Orthonormal Ground

The rotation matrix sends the point (1,0) to (cos(10),sin(x)) and the point (0,ane) to (-sin(ten), cos(ten)). The standard basis eastward₁=(1,0), e_two=(0,i) is an orthonormal basis, pregnant that
e_ane.due east_one=1 (check: 1.one+0.0=ane)
e₁.e₂=0 (bank check: 0.1+1.0=0)
e₂.e₂=1 (check: 0.0+1.one=ane)

Since a rotation is a "rigid motility", it will transform an orthonormal basis to another orthonormal basis. This ways that the to a higher place 3 equations will be truthful when e₁ is (cos(t), sin(t)), and eastward₂ is (-sin(t), cos(t)). The two equations e₁.e₁ = 1 and east₂.e_ii = 1 are each a restatement of cos²(t) + sinⁱⁱ(t) = 1, while e_i.e₂ = 0 is a statement of the identity cos(t)(-sin(t))+sin(t)cos(t) = 0. Strangely enough, even the east₁.e₂ statement is a manifestation of the identity, as is shown below.

Combinatorial Identities

Another way to look at the identity is via the ability series expansions of cos(ten) and sin(x).

cos(x)

ane

x^two/2!

x⁴/iv!

x^half-dozen/6!

ten⁸/8!

…

sin(x)

10^three/3!

ten⁵/5!

x^seven/7!

…

This ways that

cos²(ten)	=	1	-	(ane/ii! + one/ii!)	10²	+	(i/4! + 1/2!2! + i/4!)	x⁴/4!	-	…
sin²(x)	=				x²	-	(1/three! + 1/iii!)	x^iv/iv!	+	…

In this context, the identity cosⁱⁱ(t)+sin²(t)=1 is really encoding an space number of identities involving factorials, namely

1/2! + one/2!	=	1
1/4! + 1/two!ii! + 1/iv!	=	one/3! + 1/iii!
1/six! + 1/4!two! + 1/2!4! + 1/6!	=	1/5! + 1/3!three! + 1/5!
	…

These identities can be reexpressed in terms of combinatorial coefficients ( ^northwardC_r = due north!/(n-r)!r!)

²C₀ + ²C₂	=	²C₁
⁴C₀ + ^fourC_two + ⁴C_four	=	⁴C_i + ⁴C₃
⁶C₀ + ⁶C_two + ⁶C₄ + ⁶C₆	=	⁶C₁ + ^{half dozen}C₃ + ^sixC_v
	…

These are maxim that the even combinatorial coefficients sum upwardly to the aforementioned effect as the odd combinatorial coefficients. This result tin be proved directly. Information technology is about easily seen by looking at Pascal'south triangle, and calculation the terms in a row in 2 different ways. Furthermore, using the ability series expansions to extend the definition of cos and sin to the complex numbers, nosotros now know that the identity is true for complex t. Thanks to Bob Uva for pointing this out.

Exponential Office

Continuing along these lines, the fact that
	e¹⁰	=	1 + x + 10²/2! + x³/3! + x⁴/iv! + …
immediately tells us that
	e^ix	=	1 + ix - 10ⁱⁱ/2! - 9ⁱⁱⁱ/3! + 10^four/four! + …
which is, splitting into the even and odd powers
	e^ix	=	cos(x) + isin(ten)
At this bespeak there are two means to get to the identity.

Algebra

The first is to realize that the single equation e⁹ = cos(x)+isin(10) gives us the equation e^-9 = cos(x)-isin(x) and from these two equations we tin solve for cos(10) and sin(10) to get
cos(ten) = (e^ix+east^-nine)/ii
sin(x) = (e^nine-e^-ix)/2i.
Letting w represent e^ix , and then that 1/w is e^-ix , we have that cos²(x)+sin^two(x) is (west+i/w)²/4 - (due west-1/due west)²/4. This simplifies to one. Then the trigonometric identity can be viewed every bit the algebraic identity (w+1/w)² - (w-1/w)² = iv.

Factorization

The second is to exist clever (in a different fashion), and realize we can factorize a² + b² as (a-ib)(a+ib). If you haven't seen this before, it'due south a restatement of aⁱⁱ-b² = (a-b)(a+b). Using complex numbers, we take that -b^two is (ib)² , which leads to aⁱⁱ+b² = a²-(-bⁱⁱ) = a² - (ib)² = (a-ib)(a+ib). Incidentally, it's of form as well true that a²+b² = (b-ia)(b+ia). Anyway, applying the factorization to cos²(x)+sinⁱⁱ(ten), we get (cos(ten)+isin(x))(cos(x)-isin(x)), which is e^ixe^-ix . Using w to stand for e^ix , the fact that cosⁱⁱ(x)+sin²(x)=1 is only a convoluted way of saying w(one/w)=1.

Parametrized Curve Derivatives

Consider the parametrized curve c(t) = (cos(t), sin(t)). The identity tells the states that this parametrized curve is always on the unit of measurement circle well-nigh the origin. Differentiating, nosotros accept c'(t) = (-sin(t), cos(t)) . c'(t).c'(t) is (-sin(t))(-sin(t)) + cos(t)cos(t), which is merely cosⁱⁱ(t)+sin²(t). The fact that this is 1 tells us that the parametrized curve is actually parametrized by arc length. So, the trigonometric identity tin exist viewed every bit just stating the fact that radians traverse the unit circumvolve at unit speed. Finally, differentiating once more, we get c''(t) = (-cos(t), -sin(t)). Apparently, c''(t).c''(t) = cos²(t) + sin²(t), then that the identity tells us that moving uniformly along the circumvolve results in an dispatch of constant magnitude.

Integral

Finally, another arroyo to establishing that cosⁱⁱ(ten)+sin^two(x) is ane is to realize that it is really stating two separate backdrop, namely that cos²(ten)+sin²(x) is a constant, and that the constant happens to be one, ie. for some value of x, cos²(ten)+sin²(10) is ane. The latter property is quickly established: taking x=0, cos(x)=one and sin(10)= 0. Clearly 1²+0² =1.

Given a function f, to establish that f is a constant function, information technology suffices to constitute that the derivative of f is zero. Applying this technique to f=cos²+sin² , the first pace is using the chain rule to go that the derivative of cos²(x)+sin²(10) is 2cos(10)cos'x + 2sin(10)sin'(ten). Via the derivative identities cos'(x) = -sin(ten), and sin'(ten) = cos(10), we have that 2cos(x)cos'x + 2sin(x)sin'(x)simplifies to 2cos(x)(-sin(x)) + 2sin(10)cos(x) , which is zip. So the identity tin can exist viewed as the integrated version of the petty identity
cos(x)(-sin(x)) + sin(x)(cos(x)) = 0, which we saw earlier in a completely different context.

Conservation Of Energy

Yet another mode to see that the cosⁱⁱ+sin^two is constant is to realize that it represents the sum of the potential and kinetic energies of the solution x=cos(t) to the equation for unproblematic harmonic move x''(t)+ten(t)=0.

For a particle of mass ane, the kinetic energy is (1/two)x'(t)ⁱⁱ , and the potential energy is (one/2)10(t)² (upto an additive abiding). Conservation of free energy tells usa that (1/2)10'(t)²+(1/two)x(t)ⁱⁱ is a constant, and so ten'(t)²+ten(t)^two is also a constant. Taking the solution 10(t)=cos(t) (or x(t)=sin(t)) we get the identity.

I should mention that none of the above mathematics is dependent on the underlying physics. If 10(t) is a solution to the second guild equation x''(t)+F(10(t)) = 0, and so (1/2)x'(t)² + Five(10(t)), where 5 is an antiderivative of F, is constant. Uncomplicated differentiation extablishes this.

Incidentally, since x(t)=acos(t)+bsin(t) is the full general solution to the second order equation, we have that
(acos(t)+bsin(t))²+(-asin(t)+bcos(t))² is the abiding a^two+bⁱⁱ

Hyperbolic Analogues

The next step to understanding the identity is to compare and contrast it to the identity for hyperbolic cosine and hyperbolic sine, namely cosh²(t) - sinh²(t) = one. I'll defer this to a later essay.

April two 2003	Posted
April vii 2003	Concluding Updated